See the Sun from Other Stars – Sky & Telescope

[ad_1]

Observing the stars — Every star we see in our night sky also has a view of the Sun in its sky. We’ll visit eight of these locations for a fresh perspective on our familiar digs.
*Bob King*

Something like 9,100 stars are visible with the naked eye across the entire planet. Each appears in a particular constellation and shines with a specific magnitude, unless it’s a variable star like Algol, in which case its brightness varies. From each one of these stars we might imagine looking back towards the Sun, which shines in each of their skies as surely as they do in ours.

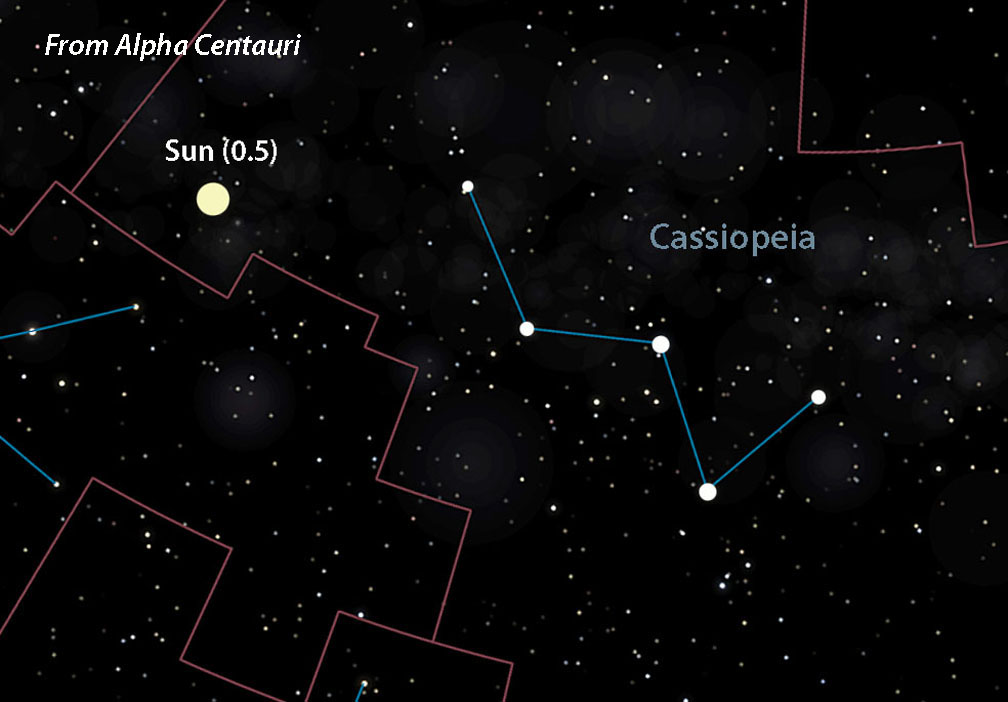
Depending on that star’s distance from us the Sun may appear bright or faint. From the neighboring star system Alpha Centauri, 4.4 light-years distant, it shines at magnitude +0.5, nearly as bright as Procyon in Canis Minor. But from far-flung Deneb at about 2,600 light-years you’d need dark skies and an 8-inch telescope to spot the 14.3-magnitude speck.

Winter can be confining. Maybe that’s what inspired my desire to figuratively leave the solar system and see it from other points of view. This got me wondering how bright the Sun would be and in what constellation it would appear when viewed from a planet — imaginary or real — orbiting one or more of the familiar bright stars?

Sun from Alpha Centauri — From the Alpha Centauri system’s distance of 4.4 light-years, the Sun shines at magnitude +0.5, nearly as bright as Alpha Centauri (magnitude 0.0) appears in Earth’s sky. Observers there would see it as the brightest star in the W of Cassiopeia, which at this distance, appears only slightly distorted from its appearance back on Earth.
*Celestia (with additions by Bob King)*

Magnitude mastery

First, we’ll need to calculate the Sun’s apparent magnitude from a specific distance. For that you’ll use the formula for determining a star’s absolute magnitude but solve for apparent magnitude instead. Here’s one iteration of this gem of mathematical magic:

m-M = 5 log(d/10)

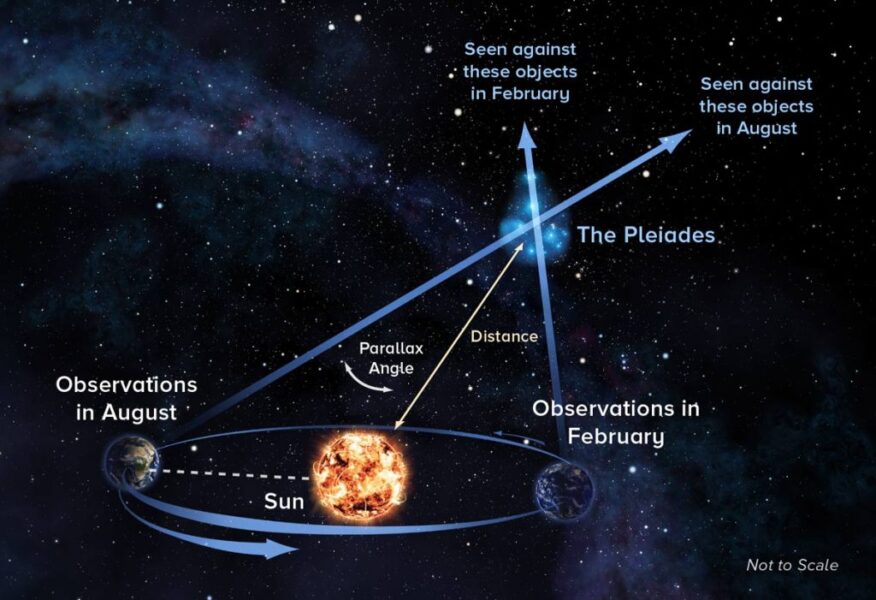
We’ll have to plug in M = absolute magnitude of the Sun and d = distance to a star of our choosing in parsecs. Once we know these values, we can do the math to find m, the Sun’s apparent magnitude at the distance of that selected star.

The Sun’s absolute magnitude, M, or how bright it would appear at a standard distance of 10 parsecs (32.6 light-years), is the easy one to plug in since we already know it. Absolute magnitudes provide a standard reference for directly comparing stars’ true luminosities. The Sun has an absolute magnitude of 4.8, a considerable step down from its apparent brightness of 26.7!

Parallax explanation — Astronomers measure distances to relatively nearby stars (e.g., the Pleiades shown here) using a technique called *trigonometric parallax*. When viewed six months apart from opposite sides of Earth’s orbit, the object shows an apparent shift in position (parallax) against the much more distant background stars. Using simple geometry its distance can be determined. Land surveyors use the same triangulation technique . . . with smaller baselines, of course!
*NRAO / AUI / NSF*

Please pass the parsecs

It’s easy to look up a star’s distance (d), but depending on your source, you might find it quoted in light-years — and so you’ll have to convert to parsecs. A parsec is equal to 3.26 light-years, which is the distance at which the radius of Earth’s orbit subtends an angle of one arc-second. A star located one parsec away would have a parallax of one arcsecond. Proxima Centauri, the closest star to the Sun, has the greatest parallax, equal to 0.77 arcsecond.

Sun from Barnard's Star — From Barnard’s Star at a distance of 6.0 light-years, the Sun (magnitude 1.1) is situated on the Orion-Monoceros border. It joins Rigel, Betelgeuse, and Sirius in a bright asterism we might dub the “Tetrahedron.”
*Celestia (with additions by Bob King*)

Many online converters will help you make parsecs out of light-years. I found this one straightforward, mostly ad-free, and with a host of fascinating options, including a conversion from light-years to cubits! (If you’ve never heard of a cubit, it’s an ancient unit of measure equaling the length of the forearm from the elbow to the tip of the middle finger . . . it’s derived from the Latin for “elbow,” in fact.)

Good one-stop shops for stellar distances include the Abrams Planetarium list of the 100 brightest stars or any recent volume of the Royal Astronomical Society of Canada’s Observer’s Handbook.

Now you have everything you need to solve for the Sun’s apparent brightness from your star of choice. Copy and paste the equation into an equation solver (OK, I’m lazy), put in the values for M and d (remember, it’s parsecs only), and out comes m. So much fun. I use MathPapa, but there are many others.

Sun from Sirius — Traveling 8.7 light-years to Sirius, distance and viewpoint combine to shift the positions of relatively nearby stars like Altair, which distorts the familiar constellation’s shape. The Sun also fades to magnitude 2.0, about as bright as a Big Dipper star. In a few cases, the software (see below for details) provided magnitudes of other bright field stars, in this case Altair. From Earth Altair shines at magnitude +0.8 but fades to 1.6 at Sirius.
*Celestia (with additions by Bob King)*

Sunshine at Arcturus

Here are some examples of the Sun’s apparent magnitude as seen from some familiar stars:

Alpha Centauri = +0.5
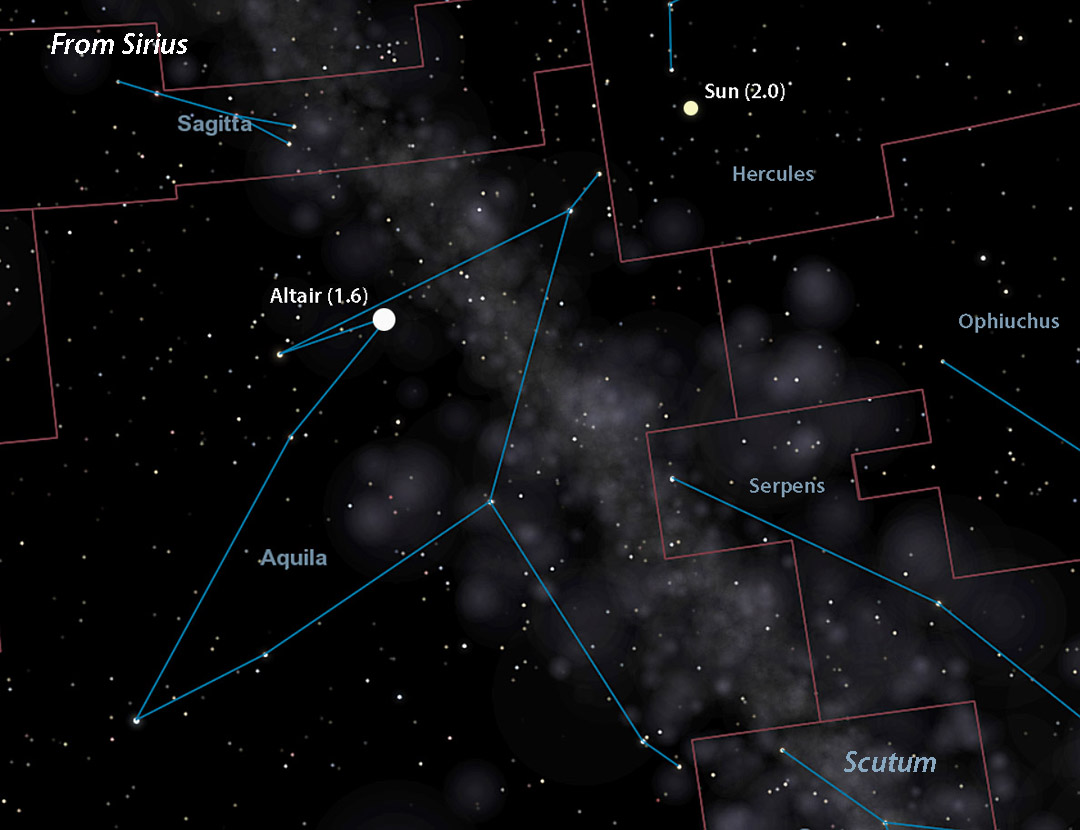
Sirius = 1.9
Procyon = 2.5
Altair = 3.4
Vega = 4.2
Pollux = 4.9
Arcturus = 5.1
Capella = 5.4
Aldebaran = 6.3
Regulus = 6.7
Spica = 9.3
Antares = 11.0

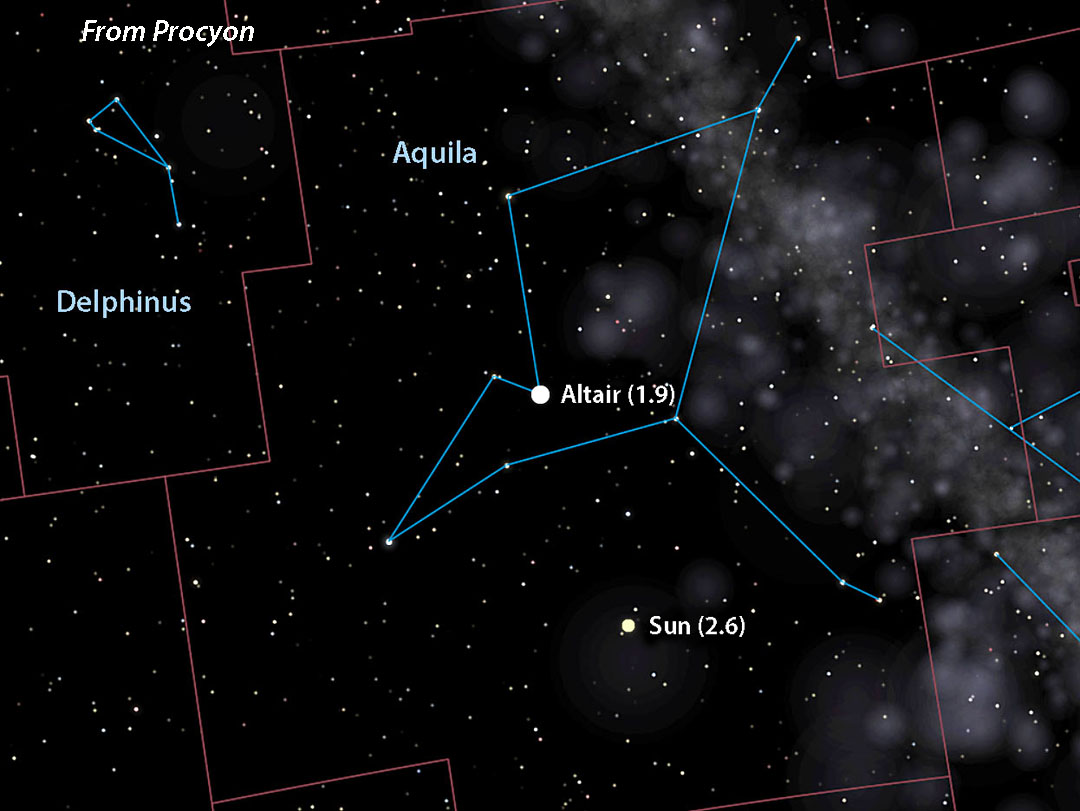
Sun from Procyon — From Procyon in Canis Minor (distance 11.4 light-years) the Sun has faded to magnitude 2.6. Distortions in the shapes of Aquila and Delphinus are apparent.
*Celestia (with additions by Bob King)*

Once we know the Sun’s apparent brightness, we’ll next want to recreate its appearance from an alien star system’s sky. For that we’ll need two things: its celestial coordinates as seen from the star and the positions of familiar stars and constellations from the point of view of an observer at that location.

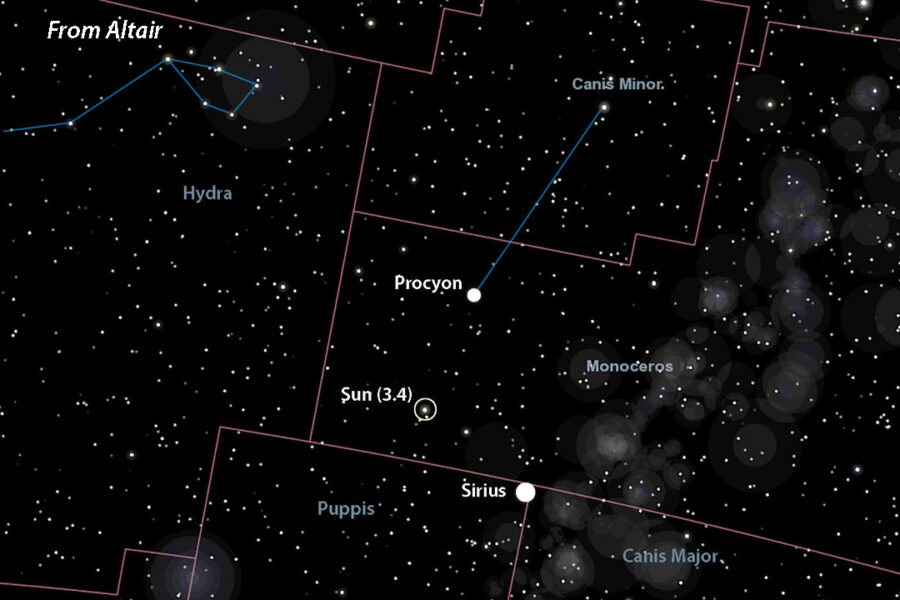
Sun from Altair — From Altair’s distance of 16.7 light-years, the Sun shines modestly at magnitude 3.4 in a much-elongated version of Canis Minor.
*Celestia (with additions by Bob King)*

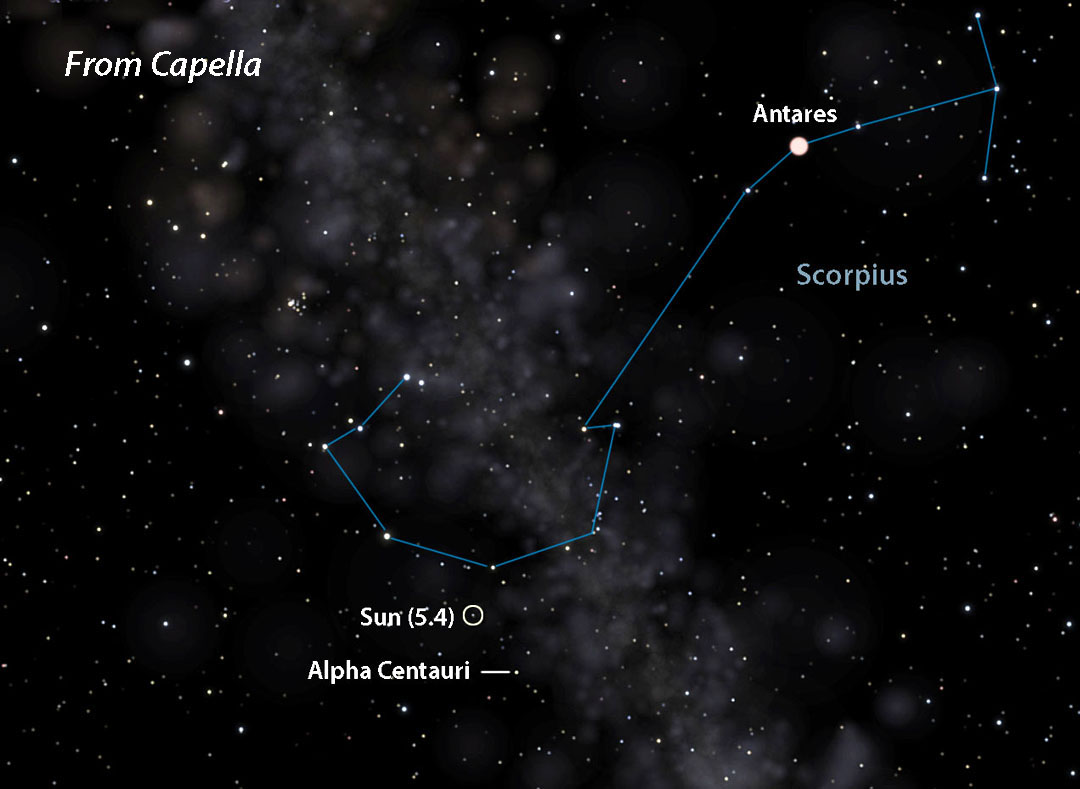
Let’s choose Sirius, located at R.A. 6^h 45^m, Dec. –16° 43′. To find the point in the sky directly opposite Sirius — where you’d see the Sun from that star — just add 12 hours of R.A. and reverse the declination sign. That puts the Sun (now 2nd magnitude) at R.A. 18^h 45^m, Dec. +16° 43′ in southeastern Hercules. If adding 12 hours to the R.A. shoots it past 24 hours, subtract 24 from that number for the correct right ascension.

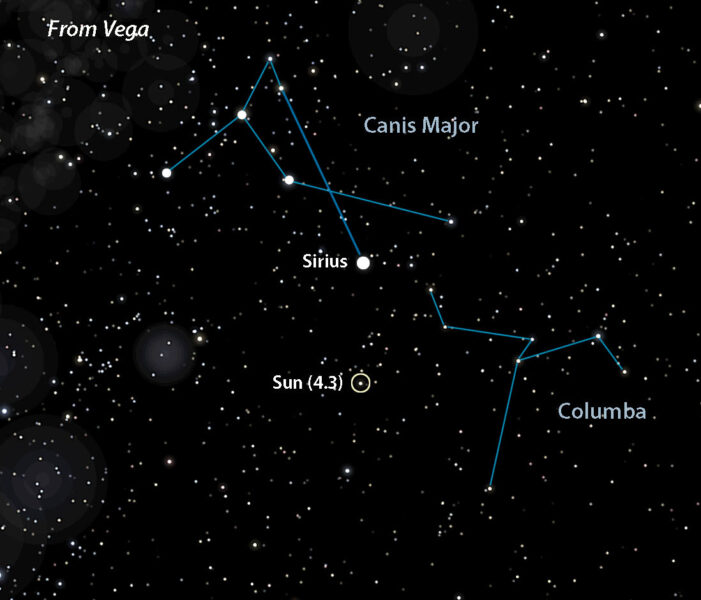
Sun from Vega — The Sun takes a little more effort to find in Vega’s sky 25 light-years distant. It glows at magnitude 4.3 just east of the Columba and south of a “folded” Canis Major. Sirius shines nearby to assist.
*Celestia (with additions by Bob King)*

A crushed teapot?

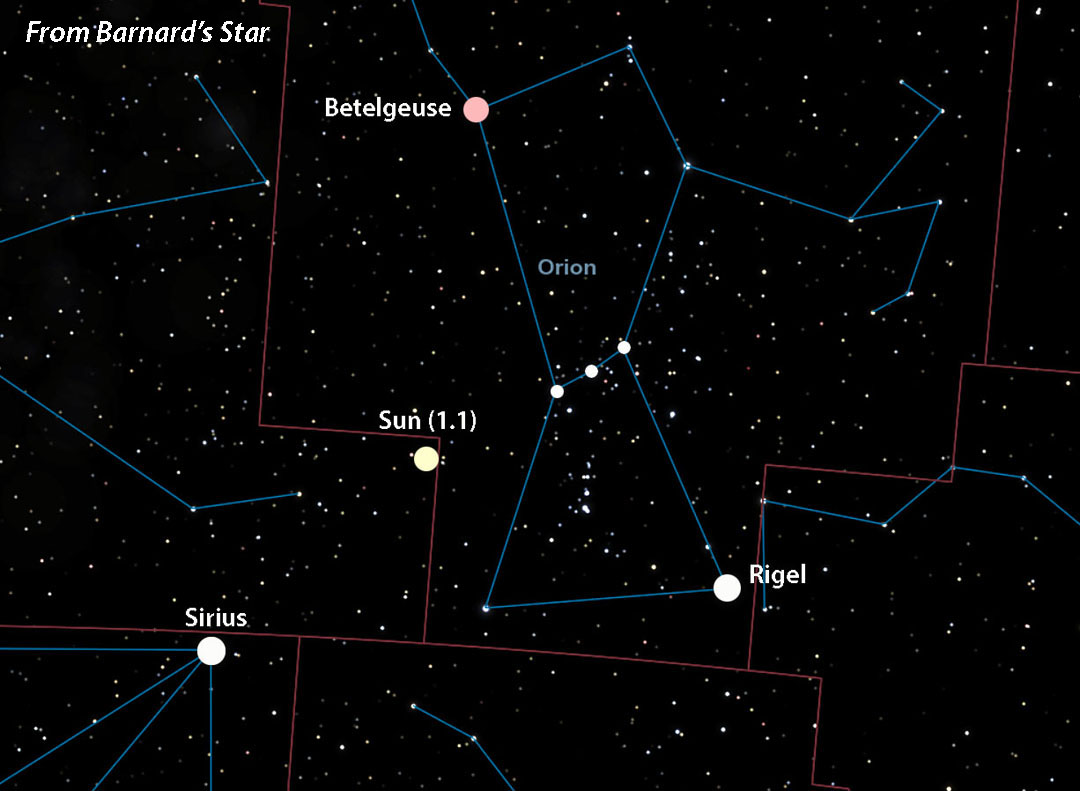
Although stars appear pasted on a flat sky, space is obviously three-dimensional — 4D really, but three will do for our purposes. When you jump from one star to another, its neighbors also shift around. This can seriously alter a constellation’s outline compared to the view from Earth. The farther you travel, the more bent out of shape the constellations become. To prevent warp-overload I chose only relatively close stars. Once you get beyond 50 light-years or so, depending on the region of the sky, star patterns and their magnitudes quickly become unfamiliar. In fact, I was amazed at how malleable the patterns were given the relatively modest distances I “traveled.”

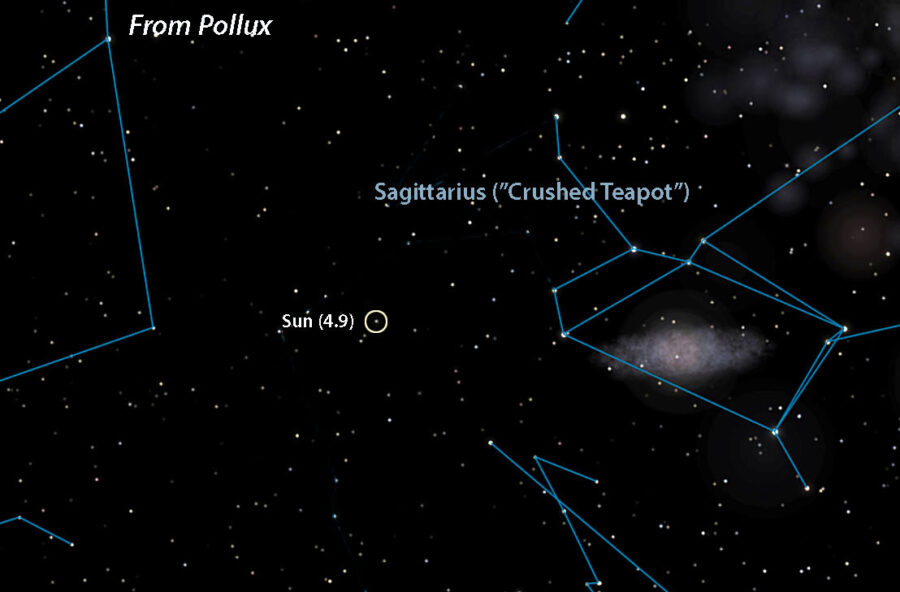
Sun from Pollux — Both Sagittarius and the Sun might be difficult to recognize from Pollux 33.7 light-years away. The Sun would appear as a faint, naked-eye star at magnitude 4.9 from Thestias, a Polluxian planet at least twice as massive as Jupiter that orbits the orange giant star every 1.6 years.
*Celestia (with additions by Bob King)*

For my mode of transportation I chose the free space simulator Celestia, which is available for Windows, Linux, macOS, iOS and Android. I had to play around with it a bit and add a few of my own enhancements, but it does a great job plotting the Sun’s location from when you’re far at home. Be aware that its range of “dot” sizes to depict stars is limited, so I tried my best to represent the Sun and other key stars as you’d see them visually. Please take these representations with a grain of interstellar dust.

Sun from Capella — The Sun and Alpha Centauri are neighbors below the tail of Scorpius from Capellan skies at 42.9 light-years away. From here the Sun is still faintly visible with the naked eye.
*Celestia (with additions by Bob King)*

The jaunts were not only fun and instructive, but if there was any Sun-centered, lingering Copernicanism left in my veins when I began this journey, I arrived home more unmoored than ever. Not that that’s a bad thing. Picturing the Sun’s place in the firmaments of its fellow suns opened up my mind to what it means to be a star among many.